
|
||
| Copyright 2017 CNES-CNRS | ||
|
||||||||
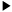  Database Access Database Access------------------------  HOME HOME What's new ? What's new ? Graphical tool Graphical tool  GEISA 2015 (new) GEISA 2015 (new) GEISA 2011 GEISA 2011  GEISA 2003 GEISA 2003 |
by A.N. Rublev (Internal Note IAE-5715/16 of Russian Research Center " Kurchatov Institute ", Moscow, 51 pp., 1994). Extended abstract Aerosols are known to influence the propagation of the solar radiation in the atmosphere. Aerosols emission sources are numerous: e.g. dust storms, fuel combustion (soot), ocean sprays, etc... Stratospheric aerosols and tropospheric anthropogenic aerosols which play an essential role in climate forcing (Charlson et al.1) can be generated by atmospheric chemical reactions with sulfates, sulfuric acid and nitric acid. The volcanic eruptions are one of the important atmospheric aerosol generators, for example the eruption of the volcano Pinatubo, Philippines, June 1991 resulted in the emission 20 Mts of SO2 (Gregs et al.2) which is a main source of sulfuric acid aerosol fraction. Despite the large number of different aerosol sources, only some selected basic aerosol components have been considered in the development of various aerosol models (WMO publication3). Principal aerosol models (e.g. continental, urban, maritime, stratospheric, volcanic, upper atmosphere, and cloudy) and their basic components (e.g. dust, water-soluble particles, soot, salt particles (oceanic), sulfuric acid solution droplets, volcanic ash, and water) are listed in Table 1 (from Ref. 3) with the following entries:
• the scattering coefficient:
• the scattering phase function corresponding
to the scattering angle
q:
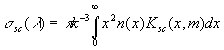 (1)
(1)
• the extinction coefficient: 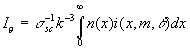 (3)
(3)• the single scattering albedo: • the asymmetry factor: • the normalization factor: x=kr is the dimensionless size of the particles with radius r m=p-iq is the complex index of refraction with the real (p) and imaginary (q) parts n(x)-is the aerosol particle size distribution function (i.e., n(x)d(x) is the number of particles per cm3 with dimensionless radii x in the interval dx so that 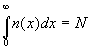 is
the total number of particles per cm3); is
the total number of particles per cm3);
Ksc(x,m)and Kex(x,m) are dimensionless efficiency factors for scattering and extinction, respectively (Ref. 4) i(x,m,q) is the scattering intensity for non-polarized radiation (Ref. 4):
is a linear interpolation of the phase function Iq..
where tgas is the atmospheric gases optical thickness calculated using, for example, well-known spectroscopic " line-by-line " methods; taer is the aerosol optical thickness calculated for an arbitrary non-homogeneous path L:
It should be outlined, that the normalization factor of Eq.(6) ( The Mie theory (see, for example, Deirmendjian4, Van de Hulst6) based algorithm has been developed and a related computer code as well, providing a reliable accuracy for computations of the above mentioned aerosol optical properties (estimated relative error £ 0.3%). Main results presented in the publication are (see Table 2 as an example): • Tables in the Appendix to the paper provide the computed values of the phase function for the principal aerosol models and their basic components as listed in Table 1. The calculations were made for 8 wavelengths in the UV, visible and IR regions, with an estimated relative error £ 0.3%. • The principal optical properties of the basic aerosol components (column
2 of Table 1: soot, dust, water-soluble particles, etc...), namely • The same as above defined optical properties for non-cloudy basic aerosol models (column 1 of Table 1: continental, maritime, urban, etc...). As an example, results of the calculations for the urban aerosol model with basic components from Table 1 (water-soluble, soot, dust) are shown in Table 2. • The optical properties for a cloudy aerosol model with a particle number concentration N0=353.678 cm-3 corresponding to a typical cloud water content W=0.3 g m-3 (Ref. 7), with the modified Gamma function n(r) (Ref. 6, 7) as a particle size distribution function: The software package AERCOMP (FORTRAN code) allowing the determination of the optical properties of more complex aerosol models has been developed. In particular, using optical properties of basic aerosol components, one can calculate (applying linear interpolation on wavelengths and cosines of scattering angels) the optical properties for more complex, composite aerosol models. Table 2 is an example of outputs of this program. References
(from Ref. 3)
Table 2. Integrated optical properties of the urban aerosol model (a non-cloudy model).
l - wavelength in micrometers; sex - extinction coefficient in km-1; w- single scattering albedo; m- asymmetry factor; Ka- normalization factor.
|
||||||||||||||||||||||||||||||||||||||||||||||